Binary

The numbers that you are most likely familiar with are the decimal (base-10) system, i.e., the digits 0 through 9. The binary system is a base-2 system that uses only “0s” and “1s” to represent all numbers.

Example

For example, the binary number “100” is the same number as the decimal number “4.”

Think about a light bulb, how many ‘states’ can it have? What about 2 Light Bulbs in a row?

1. OFF, OFF (0)
2. OFF, ON (1)
3. ON, OFF (2)
4. ON, ON (3)

4 states total! (Counting from 0 to 3)

Computers use binary information

The computer converts all of its information into binary before doing computations. Thus, it is important to understand the basics of binary, so we know how to interpret common computer data representations.

In the base-2 system, positional values are denoted as 2ⁿ, where n is the position. “n” values begin with 0 and increase from right to left.

Example:

Base-2 from the 0th power to the 6th power:

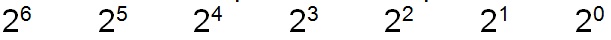
Taking into account the base-10 equivalent values gives:

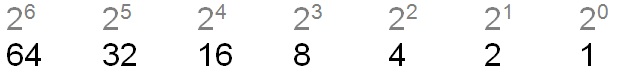
Example
Binary string “1001”:

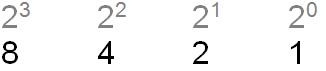
The decimal equivalent would be: 8+0+0+1 = 9

The binary string shows that there are “1s” at 2³ and at 2⁰, and the “0s” at 2² and 2¹ indicate that we do not include those numbers in our total. They are significant placeholders, however, and cannot be discarded without changing the value of the string: “11” in binary being equivalent to “3” in decimal.

Example
Converting decimal to binary “26”:

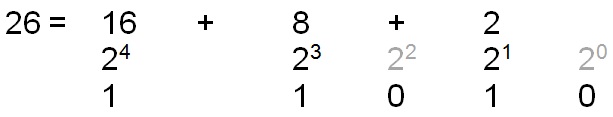
The binary equivalent would be “11010.”

Bits and Bytes:

Rather than digits we refer to the bits (binary digits) of a number. Each binary position represents bit (b), whether that position is occupied by a “1” or a “0.” An individual bit is typically too small to represent sufficiently larger values. To efficiently process information, computers handle groups of bits. The smallest group of bits processed by a computer is a byte (B), which is 8 bits long.

Software Amount

The standard amount of anything (watts, joules, etc.) with a giga- prefix is 10⁹ (1,000,000,000), counted in the decimal system. Computers often express storage using binary multipliers, so a gigabyte (GB) is 2³⁰ (1,073,741,824 in decimal) instead.

Large numbers of bytes are referred to using the International System of Units (SI) prefixes, with those prefixes using a base-2 count rather than the base-10 count. This means that binary-based prefixes do not represent the same amount as base-10 SI prefixes.

Example:

How many bits (b) are in a Gigabyte (GB)? 

(1024³)*8 = 8.6×10⁹ b in 1 GB

ASCII

Binary can be converted to the commonly used ASCII codes. ASCII is based on 128 symbols (10 numbers, 26 letters of the English alphabet, some punctuation marks, etc.), and it represents visible characters or commands. The original ASCII table is encoded on 7 bits, and therefore it has 128 characters. Nowadays, ASCII is often extended to 8 bits.

You can type man ascii into a terminal to get a list of the codes. On the Eos machine, you’ll a table with a header like this:

Oct   Dec   Hex   Char

with a table. One line is presented from the table here — we see that the hex value of the letter w is 77.

167   119   77    w

If you use the terminal on your personal machine, you may see a different formatting for the output.

Summary

• Binary is a positional number system using 1 and 0.
• referred to as ‘Base 2’ or with a subscript 2
• 8 bits = 2⁸ = 256 possible values, 255 is largest number
• Store data and control components
• Bits (b), bytes (B), kilo-, mega-, giga-, tera- for this class we use the software amount